How to create a smooth spherical room

[dejime]

I’m trying to create a room with this kind of cross section:

Initially I wanted to do it with LatheGeometry, but I don’t like the topology it produces.

My current naive approach is to create an IcosahedronGeometry, translate its vertices up a bit, squish every y<0 vertex to y=0 to create a floor, and try to round the edges:

const roomRadius = 200;
let roomGeo = new THREE.IcosahedronGeometry(roomRadius, 6);
roomGeo.translate(0, 40, 0);
{
	const attr = roomGeo.attributes.position;
	for (let i = 0; i < attr.count; i++) {
		const initY = attr.getY(i);
		let y = initY;

		// Create floor
		y = Math.max(0, y);

		// Lift up vertices around the edge
		const liftedHeight = roomRadius * 0.3;
		if (initY > -liftedHeight && initY < liftedHeight) {
			y = liftedHeight * (Math.min(1, (initY + liftedHeight) / (liftedHeight * 2)));
		}

		attr.setY(i, y);
	}

	roomGeo.computeVertexNormals();
}

But rather than a spherical room as illustrated above, it is producing more of a mushroom head shape:

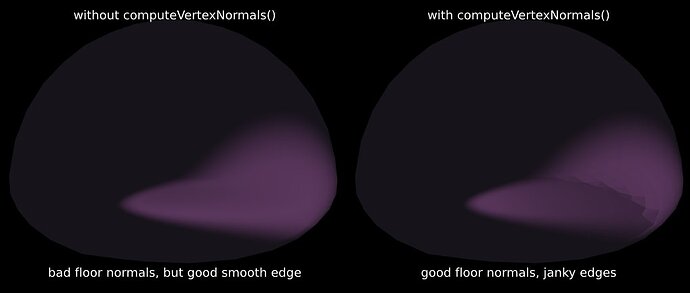
Which would be good enough, but there is also an issue with normals when I do computeVertexNormals() on the resulting geometry. I can either have a good floor, or good smooth edges, but not both:

Should I just stop being pedantic and go with the Lathe?

[prisoner849]

Just out of curiousity: why not use LatheGeometry for such type of room?

UPD Ah, oops. You have the same thought at the end of question

[kalabedo]

Is blender an option for you? such objects are pretty easy to create there. Then you just import it into threejs as a glb file. Normals can be fixed there too.

[dejime]

@prisoner849 as I’ve mentioned, I don’t like the topology LatheGeometry produces.

@kalabedo I’m not that good in blender or know how to properly work with glb’s in three yet. I’ve tried, but it’s a 31kb file, and when loaded in scene the lighting is all wrong (overexposed and seemingly ignores ambient light), and the CPU/GPU load of the browser tab rendering it doubled.

spherical_room.glb (31.3 KB)

Also if I can generate something in a couple lines of code, I’d rather not do network requests.

[prisoner849]

Tried it with toCreasedNormals() of BufferGeometryUtils: Edit fiddle - JSFiddle - Code Playground

[vielzutun.ch]

@dejime

Should I just stop being pedantic and go with the Lathe?

I’m getting consistently very good results going with a LatheGeometry for my visualisation of mechanical lathed parts of mechanisms. The reason for this is, in my view, that all vertices are situated on circular, concentrical and parallel meridians. So you can get an absolutely clean “transition meridian” between the rounded edge of your room and your flat bottom.

Very much unlike anything which you’ll get from a Icosahedron geometry. where you’re bound to get triangles, which span the transition meridian between room and floor, for which you’ll only “sqish” one vertex out of three, which is what gives you the “jagged” edges.

I’ve built a little helper function to that effect, which I’m happy to share:

function addArcToPath( centerX, centerY, radius, startAng, endAng, steps ) {
/*
This function adds the necessary points on an arc-path to the GLOBAL points[] array for use in a THREE.LatheBufferGeometry .

Input variables:

 centerX, centerY:  arc center coordinates
 radius:            arc radius
 startAng:          angle at which to start the arc. This is in degrees [°]!
 endAng:            angle at which to end the arc. This is in degrees [°]!
 steps:             number of intermediate points for arc approximation.

 */
    let delta = (endAng - startAng) / steps;

    for ( let i = 0; i <= steps; i ++ ) { // '<=' : I want both start and end points to be included

       points.push( new THREE.Vector2( centerX + radius * Math.cos( (startAng + i * delta) * PI_180 ),
       centerY + radius * Math.sin( (startAng + i * delta) * PI_180 )  )  );

     }

}

Please note, that this function merely adds to a point array, which must have been allocated before, using something like this:

const points = [ ];

For each new arc you’ll have to reset that array using something like this:

points.length = 0;

In your particular case, you’ll have to perform some trigonometric computations beforehand, in order to specify the transition vertex (and implicitely: startAng, endAng) of each arc.

In case you have an arc-to-arc transition, you may be fine with a smoothing out between any slightly mis-aligned normals at the transition vertex.

If you want to have a perfectly clear, well-defined transition between the arc adjacent to the floor, as well as a perfectly flat floor right up to the transition vertex, you’ll have to duplicate that vertex in the points[] array.

[trueshko]

Or you can use SphereGeometry, because IcosahedronGeometry provides a non-indexed geometry and so computeVertexNormals() cannot compute the smoth normals.

Edit fiddle - JSFiddle - Code Playground

[dejime]

@prisoner849 thanks! that’s a way better geometry solution that what I came up with but the BufferGeometryUtils.toCreasedNormals() is producing a pretty harsh and noticeable floor to wall transition (solution below)

@vielzutun.ch I understand what you’re saying, but the floor to wall transition on the icosahedron should be completely smoothed out with normals and shouldn’t be an issue. just to compute them properly. the reason why I don’t want to use lathe is that I’ve read too many articles that hammered into me that the figure below is a bad topology and should be avoided:

@trueshko yep I figured that out too

I finally stumbled upon BufferGeometryUtils.mergeVertices() that to my understanding converts the geo into instanced (docs don’t mention it). Either way, the result is finally a completely smooth room with correct normals

Thank you all for help!

[jrlazz]

Hi @dejime ,

Would Your room, at the end, and partially cutted, appear similarly to this image?

Or do am I really asking a fool thing?.
If so, pardon me for the post inclusion.

[vielzutun.ch]

@dejime

@vielzutun.ch I understand what you’re saying …

Apparently you don’t.

… but the floor to wall transition on the icosahedron SHOULD be completely smoothed out with normals and SHOULDN’T be an issue.

Obviously the reality must be mistaken

Famous quote from physics Nobel laureate Richard P. Feynman on that matter:

It doesn’t matter how beautiful your theory is, it doesn’t matter how brilliant you are. If it doesn’t agree with experiment, it’s wrong.

VertexNormals are computed by averaging and normalizing the FaceNormals of all faces that share a common vertex. For an undisturbed Icosahedron this should (I didn’t verify that) give perfect results, with each normal pointing exactly to the sphere’s center (or perfectly away from it).

But you are disturbing the icosahedron. By squishing one or two vertices of one or more faces that are being considered when averaging face normals. This does introduce asymmetries which become visible as “jagginess”.

To illustrate my point, I have briefly extended one of my recent projects to demonstrate the quality which can be achieved using LatheGeometries. Please note, that reflective materials are the most unforgiving when it comes to revealing even the slightest surface flaws.

Screenshot:

Fully interactive (OrbitControls) live demo uploaded to my webspace (Never mind the little steam engine at the center of the scene - I was too lazy to set up a dedicated JSFiddle):

https://vielzutun.ch/wordpress/Danni_animation/Three.js/Dome.html

Code which created the dome geometry:

// ***************** PleasureDome ****************

var smallRadius = 100;
var largeRadius = 500;
var r = largeRadius - smallRadius;
var steps = 72;
		
points.length = 0;
points.push( new THREE.Vector2( 0.0,  0.0 ) );		// floor center
points.push( new THREE.Vector2( -r,  0.0 ) );		// floor transition point to smallRadius
addArcToPath( -r, smallRadius, smallRadius, 270, 180, steps);	// 90° arc with smallRadius
addArcToPath( 0, smallRadius, largeRadius, 180, 90, steps);	// 90° arc to zenith

mesh_Dome = new THREE.Mesh( new THREE.LatheGeometry( points, 72, -Math.PI/2, Math.PI ), chromeMaterial );

mesh_Dome.position.set( 0.0, -100.0, 0.0 );
scene.add( mesh_Dome );

// ***************** Ende PleasureDome ****************

[prisoner849]

@dejime

that the figure below is a bad topology and should be avoided

As long as geometry’s topology doesn’t interfere with the getting of desired result or doesn’t make an impact on scene’s performance, I don’t care about topology at all. ¯\_(ツ)_/¯

[dejime]

@vielzutun.ch I was thinking of a property of indexed geometries, where no two vertices share the same normal and are just averaging neighbors resulting in perceptually smooth surface. That’s what I’ve meant by “should be smoothed out with normals”. Sorry I didn’t make myself clearer.

Here’s an example of prisoner849’s icosahedron fiddle before and after being turned into indexed: