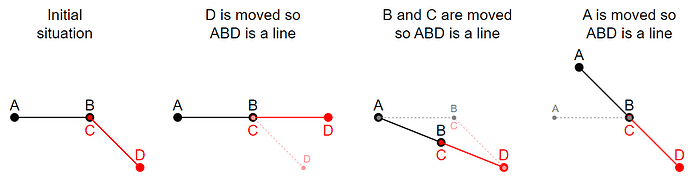
Consider these abbreviations:
- A = aPoint[n-1]
- B = aPoint[n]
- C = aPoint2[0]
- D = aPoint2[1]
Here are the required relations:
- B = C
- ABD are on one line
My suggestion was to adjust D (second image below). So the “step” from A to B is the same as from C to D (see the blue deltas in my second image in my previous post).
Of course, you can keep D unchanged. In this case adjust B/C together (3rd image); or adjust A (4th image). The point is, that you need to sacrifice some point and adjust it. I decided to sacrifice D, because I considered the first curve more important (so A and B are fixed); and within the second curve I decided the end point to be more important, that’s why I change D. You are free to change any of these points as long as you keep G1 continuity.
The solution of @prisoner849 avoids all these adjustments, as it uses only one curve and recolors a piece of it at the cost of using a shader program.
Our solutions are a nice illustration of the concept: Algorithms + Data Structures = Programs. You can achieve the same program by simple algorithm (and more complex data); or by simple data (and more complex algorithm).