I seem to have failed so far to demonstrate what the benefit of all this might be, in the context of reflection mapping. Using an obscure test geometry certainly has not helped either, I guess. So with the New Year comes a new trial! ![]()
As a real-life example I’m now using an intake valve from the ICE of my Ducati motorcycle:
which I model as a Three.js
LatheGeometry() using the following path:Although I shortened the valve stem to bring the aspect ratio of this geometry for demo purposes closer to 1.0, this sample LatheGeometry features most of the situations which one can encounter in a real life lathed part:
- cylindrical and flat circular/ring shaped sections (black)
- concave rounded sections (green)
- convex rounded sections (blue)
- conical sections (red)
- smooth transitions between different sections
- sharp-edged transitions.
So it’s a pretty versatile test geometry after all.
When it comes to reflections, even tiny deviations from the (physically) true orientations of normals have a huge impact on reflection fidelity. This impact is most pronounced in very low segment-count LatheGeometries:
See the straight red lines of the equirectangular map being rendered as zig-zag, with the “zigs” following the diagonals of the quads that are the result of
LatheGeometry().
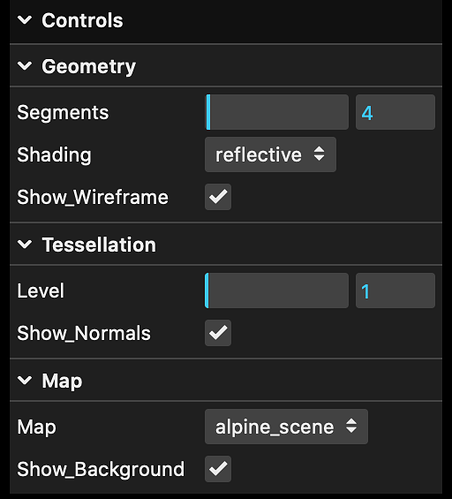
I have put together a demonstrator which allows you to
- see if there is a problem at all, and if so: how big it is.
- crank up the lathe segment count, until you reach a satisfactory reflection quality
- choose from two different maps, one photographic, one geometric
- overlay/hide a wireframe display of the geometry, to correlate display faults with quad diagonals
- show/hide a normals helper as an indicator of vertex locations
- show/hide the background map.
The most interesting part (from my point of view) is the Tessellation slider, which allows you to tessellate each quad from the “base geometry” into Level * Level sub-quads, thus simulating (preempting) the effect which a suitable shader hopefully would be able to provide. This shader would have to do a more proper interpolation of vertex normals than the currently implemented solution. See for yourself of the remarkable quality of reflections which could(!) be achieved even with very low face / vertex count LatheGeometries.
Presented as a JSFiddle: