How do you compute the smallest bounding box

Questions
,
1

Given the attached mesh, how does one compute the smallest bounding box? The mesh has no rotation.
The white area represents the current bounding box.

image
image466×791 45.3 KB

2

That’s a simple question regarding a non-trivial problem. Which is, btw, subject of ongoing academic research. Search “multivariate optimisation” for more.

4

I could have wrote a complex question but I prefer to keep it light. I can conclude there is no simple way atm. Thanks for your reply.

5

There was no offence intended re. your question. It is perfectly adequate to bring across what you are looking for. It’s just, that you happened to tap into a very deep pit …

6

Thanks for this. Yes it isn’t a trivial problem. But as I’m new to threejs I was wondering if it had something for it out of the box. Although as an alternative I was wondering if trying something such as aligning the ‘longest part’ of a mesh to an axis before measuring the boundingbox wouldn’t do better (which I have no idea how to do it yet).

7

three.js can compute axis-aligned bounding boxes and object-oriented bounding boxes. But if (as it sounds) this mesh doesn’t have any rotation — just the vertex data happens to have the shape of a rotated box — I don’t think there’s anything built in that would fit the box more tightly for you. If you could settle for a ConvexHull instead of a box, that’s an option.

1 Like
8

Let’s assume, you’re interested in the smallest (by volume) bounding box. Which depends on the rotational state of your mesh, that is: r.x, r.y, r.z, assuming it’s the mesh you’re rotating. Because Three.js can give you axis-aligned bounding boxes only.

To give you a little idea how this problem could be approached: a genetic algorithm, which is imo nothing more than a fancy word for a computerised trial&error method. It’s an iterative process, which involves the repeated introduction of “small” changes in one or more of the result-influencing parameters, in your case: r.x, r.y, r.z.

It goes like this:


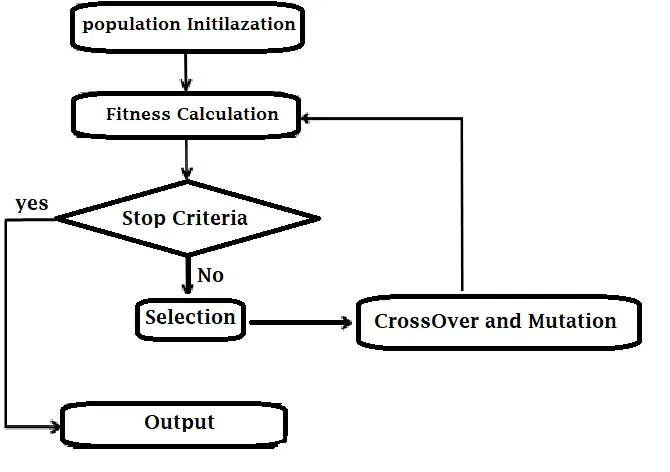
Source: https://vidyasheela.com/web-contents/img/post_img/27/GA%20Flow%20diagram.png

“Population initialisation”: your first mesh orientation which you showed us.
“Fitness calculation”: compute the bounding box volume for this set of parameters r.x, r.y, r.z .
“Stop criteria”: is it good enough? If so, you’re done.
If not good enough,
“Select” the one parameter set which you currently have.
“Crossover and Mutation”: change one parameter of this set by a small amount, i.e. r.x += 𝛆

Recompute bounding box volume.

If it has improved (become smaller than the previous one) , continue along the same direction of the last change, that is: keep increasing r.x , until you arrive at the 1st increase in bounding box volume.

If your 1st change resulted in a deterioration already, reverse the direction of your change: r.x -= 𝛆
and proceed as before.

Note, that you may get trapped in a local minimum, which may be worse than the global minimum:

Source: https://freecontent.manning.com/wp-content/uploads/evolutionary-algorithms_01.png

And then you have two more parameters r.y, r.z, which may all be inter-dependent on each other and r.x. Meaning: after doing this for r.y too, chances are, that r.x may be improved further still.

You see, it can get complicated pretty soon. That’s why I mentioned the ongoing scientific effort in this area of research. I do believe, that you can arrive at a better solution than you already have pretty quickly. Without knowing however, how far away from the best solution you end up.

1 Like
9

Thanks for taking quite a bunch of your time to give such a clear explanation on a potential solution to that complex problem! I hope I’ll have some time to try such algorithm.